The perfect frequency splitter debunked

Introduction

A few years ago, Multiplier posted a video on YouTube that grasped my attention quite a bit. In this video, he explains a technique that allows splitting the frequency spectrum into several bands without altering the phase of the combined output, meaning that when all the dry bands are played together, you get exactly the original signal back. Even though it’s true, this technique simply doesn’t work when processing the bands individually (i.e. the whole point of a frequency splitter). In fact, the higher bands contain a bunch of unwanted frequencies that are expected to be cut at the crossover points. This makes it impossible to accurately solo and process a band. Since Multiplier is quite big on YouTube and people believe what he says, I figured it would be relevant to shed some light on the subject. In this blog post, I will visually explain why it doesn’t work and then offer a working solution. Note that I will only address a 2-band frequency splitter for the sake of simplicity.

The naive frequency splitter

When implementing a frequency splitter ($n$-band), this is the first approach that usually comes to mind:

1. Create $n$ parallel chains of your signal
2. Band-pass each chain using a low pass and/or a high pass filter
3. Map the crossover frequency of the filters to some macros

The problem with this approach is that crossovers don’t have a flat amplitude response when using traditional filters (usually Butterworth). In fact, the amplitude response of a Butterworth filter is -3 dB at the cutoff frequency, which adds up to +3 dB when used in a crossover.

The standard frequency splitter

Nowadays, most frequency splitters are using Linkwitz–Riley filters. Unlike traditional Butterworth filters, their combined frequency response is perfectly flat when used in a crossover. They can simply be obtained by cascading two traditional Butterworth filters. By doing so, the amplitude response at the crossover frequency becomes -6 dB instead of -3 dB, which results in a combined amplitude response of 0 dB at the crossover point.

In other words, the crossover behaves like an all-pass filter, meaning that only the phase response is (smoothly) changed. When using filters with more aggressive slopes, the phase change can be heard by simply duplicating the dry frequency splitter a few times. However, in practice, this should be a non-issue for most people since processing is being applied to each band and the processing often messes with the phase itself. Also, when using a single frequency splitter at a time (general use case), this phase change can’t be heard by the untrained ear.

There are a lot of people arguing online that such a phase shift will wreck your mix. Yet, most are proposing solutions such as the one discussed in this post (the Multiplier splitter), which are even worst. There are indeed some phase implications of using Linkwitz-Riley crossovers (which will be discussed in another blog post), but the consensus is that you shouldn’t care. They are an industry standard and have been used for decades for this exact purpose. For mastering or phase-sensitive work, plugins will usually opt for more CPU-intensive methods such as linear phase filters to preserve phase as much as possible, as we will see later in this post.

Here are some frequency splitting VST plugins that are using Linkwitz–Riley filters:

• ISOL8 (free)
• Gaffel (paid)
• Multipass (paid)

Here are other various plugins that are using Linkwitz–Riley filters:

• ShaperBox
• Ableton’s Multiband Dynamics

Since most low-pass and high-pass filters are Butterworth, you can also build your own Linkwitz-Riley frequency splitter by using two identical low-pass filters and two identical high-pass filters chained one after the other. You can safely assume that it works with FabFilter Pro-Q in Natural Phase mode and Ableton’s EQ Eight (tested). Here are some racks I made using EQ Eight:

• Linkwitz-Riley, 24 dB slope, 2-band
• Linkwitz-Riley, 24 dB slope, 3-band
• Linkwitz-Riley, 96 dB slope, 2-band
• Linkwitz-Riley, 96 dB slope, 3-band

Otherwise, you can implement your own splitter using any EQ by following the next section, and analyze it using Bertom’s EQ Curve Analyzer to make sure it works as intended (perfectly flat amplitude response).

Linkwitz-Riley design

If you want to design a Linkwitz-Riley frequency splitter in your DAW, you can follow the following schemas.

For 3-band frequency splitters, it gets a little more complicated. We must make sure to align the phase of each band. To do so, we must redundantly apply the filtering from other bands. The additional processing behaves just like an all-pass filter.

For 3+ band designs, the implementation becomes increasingly complex when done from scratch (as you might have guessed). However, it can be easily generalized by reusing lower band splitters. Since this all comes down to syncing the phase response of each band so that when they are combined back together, their respective frequencies align properly, we can implement the 3-band design using the 2-band design exclusively.

As you can see, nested splitters can be used, but not blindly. The important part is to apply nested splitters on every sibling band to sync their phase. Note that we are ditching the splitted outputs entirely in the phase-corrected bands. Instead, we are running the splitter serially (just like a normal FX), since we are only interested in the phase side effects and not the splitting per se. This approach is a generalization of the above and can be used to implement a $n$-band splitter more easily.

Finally, each Linkwitz-Riley filter can be designed using Butterworth filters as follow:

Regarding Butterworth filters, their order determines how steep they are, or how quickly their amplitude decreases per octave. A first-order Butterworth filter’s response rolls off at −6 dB per octave. This means that a second-order filter decreases at −12 dB per octave, a third-order at −18 dB, and so on. Since Linkwitz-Riley filters are constructed by cascading two Butterworth filters of the same order, the resulting order of a Linkwitz-Riley filter will be twice the order of its underlying Butterworth.

Butterworth Order	Butterworth Slope	Linkwitz-Riley Order	Linkwitz-Riley Slope
1	−6 dB / octave	2	−12 dB / octave
2	−12 dB / octave	4	−24 dB / octave
4	−24 dB / octave	8	−48 dB / octave
8	−48 dB / octave	16	−96 dB / octave

If you want to learn more about Linkwitz-Riley filters, stay tuned for my next blog post.

The “phase correct” frequency splitter

In his video, Multiplier demonstrated that using a naive frequency splitter was messing up the phase. As a result, he wasn’t able to exactly reconstruct the original signal back. Instead, the dry frequency splitter was generating a new signal that was sounding the same as the original but had an altered phase. Then, he claimed that to fix this “issue”, you could use a phase cancellation technique to perform the frequency splitting instead.

The gist of it is simple: instead of using a low-pass filter and a high-pass filter to build the crossover, you use either one of them on both bands, invert the phase on the second band and use the result to cancel the dry signal. In other words, you filter the first band normally, and take the remainder for the second band instead of using a crossover. In theory, it allows to extract the information that was cut out by the filter exactly, which allows to reconstruct the original dry signal back perfectly. However, in practice, it fails terribly when bands are used in isolation.

Let’s suppose our signal consists of two basic sine waves of different frequencies:

+

Our goal is to split this signal and get the original sine waves back. To do so, we try the above logic and apply a low-pass filter to the signal. Because we are using low latency filters, we can expect the phase of the resulting sine wave to be a bit offset compared to the original. In fact, the closer the original signal is to the crossover frequency and the steeper the slope of the low-pass filter is, the worst the phase shift becomes.

Now, we simply need to subtract the filtered sine wave from the dry signal to recover the remainder. In theory, we should obtain the original high frequency.

However, since the phase of the dry signal is no longer in sync with the filtered sine wave, a new frequency is introduced:

As you can see, this “new” frequency looks quite familiar: it’s a phase-shifted version of the green sine wave with a weaker amplitude. More exactly, it’s the direct difference between the original green sine wave and its filtered counterpart (phase shifted).

In short, this means that phase-canceled bands will always contain some of the frequencies that were used to cancel them, and their amplitude will directly depend on the filters being used (steeper filter results in a greater phase shift).

This is of course a theoretical example with only two sine waves involved, but you can see how many unwanted frequencies might be introduced in the phase canceled band of Multiplier’s “phase correct” frequency splitter. This is audible and measurable just by soloing the said band. Sure, you can reconstruct the original signal that way, but the band doesn’t hold the expected information in isolation, which defeats the whole purpose of using a frequency splitter to process bands independently.

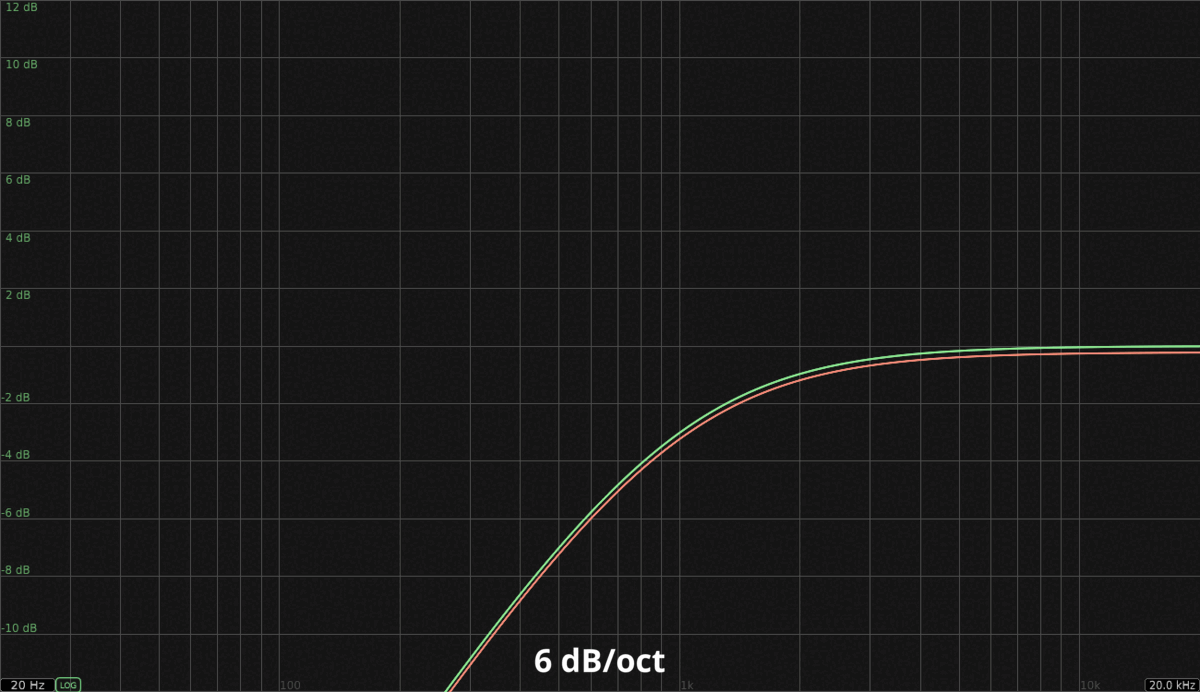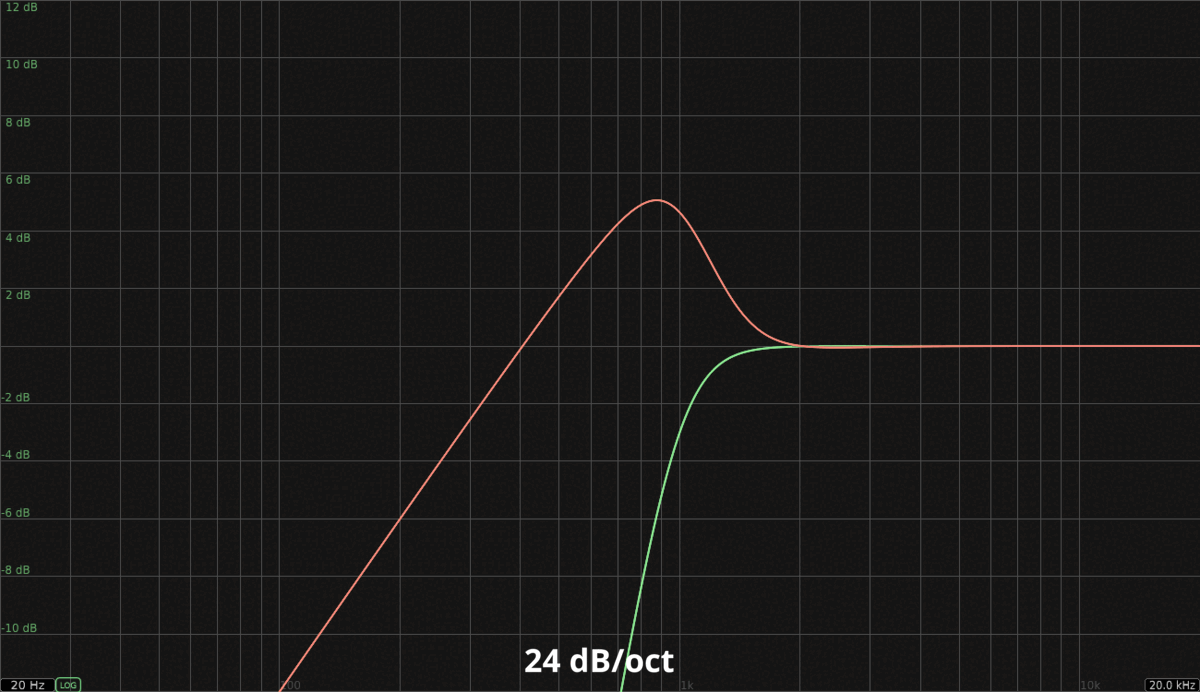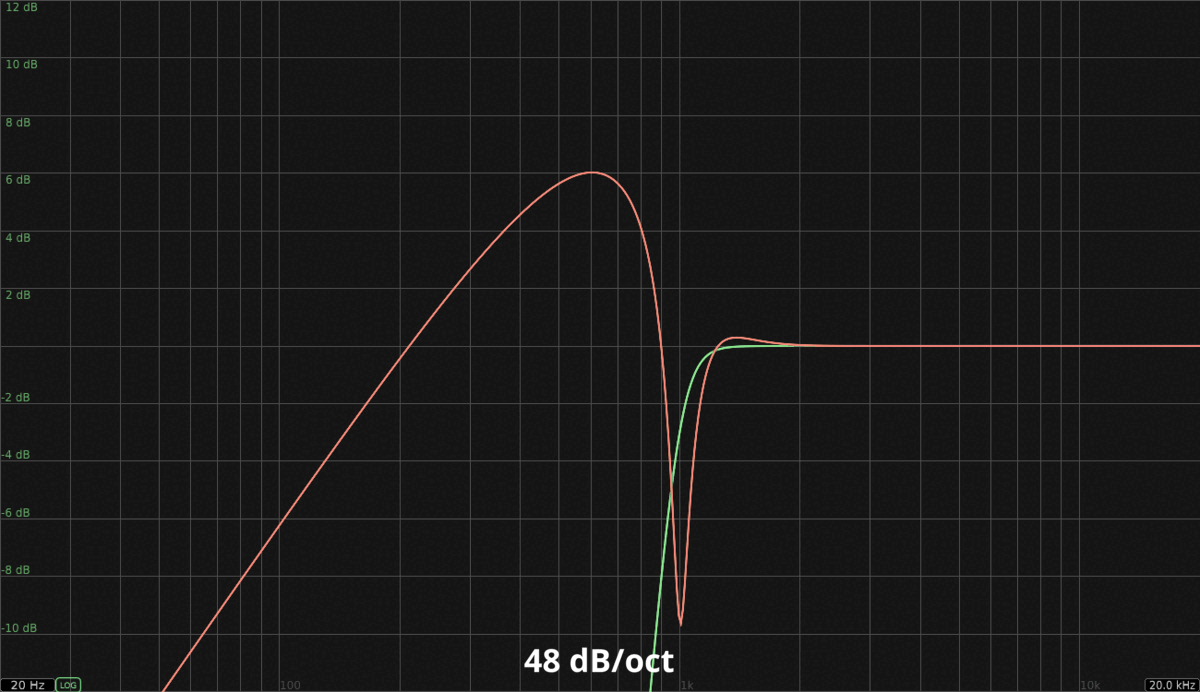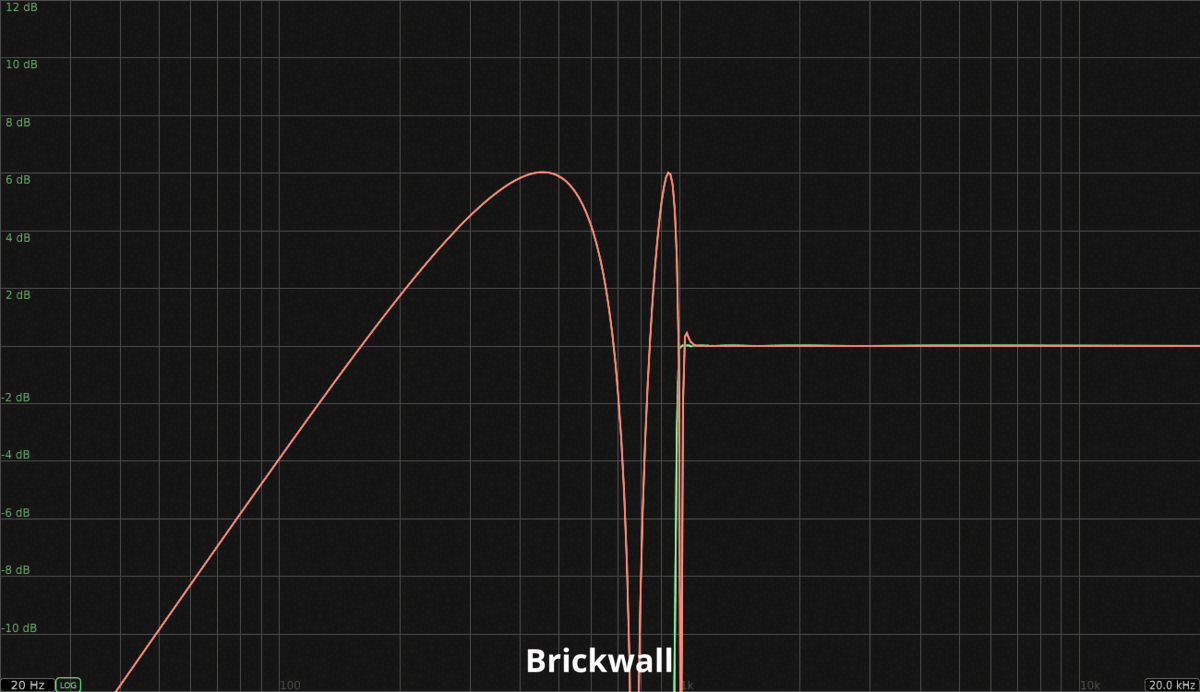
Let’s take a look at a white noise example. For the sake of the example, I have used Linkwitz-Riley filters (24 dB slope) to perform the filtering instead of single Butterworth filters (like in the original design). That way, expectations are more accurate, and the underlying issue is emphasized (two phase shifts instead of one). The crossover frequency is 1000 Hz.

As you can see (and hear), the phase canceled high band is not even remotely close to its expected counterpart. White noise is the worst possible case since it contains all the frequencies in the spectrum, but the result will be similar no matter what. Here’s the expected frequency response of each high pass filter slope available in FabFilter Pro-Q 3 (in green) compared to their actual frequency response obtained by phase canceling the corresponding low pass filter (in salmon). In theory, both curves should be matching *:

* FabFilter’s Zero Latency mode was used when capturing these graphs. In this mode, filters are approximated to maximize efficiency (no latency), which means the resulting frequency response won’t always match its analog reference perfectly. If this is important to you, the Natural Phase mode can be used instead, at the cost of latency.

Note that a popular Max for Live device called Invisible Band Splitter doesn’t suffer from the same issue. It uses hardcoded 6 dB / octave slopes, which results in a perfect filter inversion (as you can see in the GIF above). This unique property is exclusive to first-order low-pass and high-pass filters (single-pole) such as the ones used in this device, making them a viable alternative to using linear phase filters (discussed in the next section). However, the resulting 6 dB / octave slope is very low and doesn’t allow any sort of precise splitting (especially in the lower frequencies). So try to avoid this device as well if you want properly isolated bands with minimal overlap.

The almost perfect frequency splitter

To make the phase cancellation trick work as expected, we would need an EQ that doesn’t change the signal’s phase. It is known as a linear phase EQ, and several VST plugins currently on the market support this feature (FabFilter Pro-Q 3, DMG EQuality, etc.). If we refer to the figures above, we can see the linear phase version results in an almost null cancellation, meaning no additional frequencies are being introduced by the process. One would think that we could maybe implement the standard Linkwitz-Riley frequency splitter using linear phase filters without any phase cancellation trick, but there are a few drawbacks to keep in mind when using linear phase filters.

First, it causes pre-ringing, which is some sort of backward echo that softens the transients. Since this is not the point of this post, I won’t delve into much more details (Google is your friend), but keep in mind that more aggressive filters (high slope, high Q, high latency) in the lower end of the spectrum tend to cause more pre-ringing. However, pre-ringing is usually heard when boosting (e.g. bell shape) and less when cutting (crossover). So for our use case, the impact of pre-ringing is usually minimal.

Second, it may introduce some low-frequency imprecisions when used in a low enough crossover. FabFilter Pro-Q lets you choose different processing resolutions, which result in different linear phase filter delays. The greater the delay, the better the response in the low frequencies, at the cost of more pre-ringing. The lesser the delay, the worst the response in the low frequencies, at the benefit of less pre-ringing. Steeper filters will also result in greater imprecisions. To compensate, longer delays must usually be used when low-frequency precision is paramount.

Finally, as you might have guessed, it introduces a noticeable delay. This might be fine for the final mastering stages but is often not viable in a live context where MIDI input is involved (low latency). That’s why it’s usually never used for individual track processing.

So, the almost perfect frequency splitter should be implemented using the proposed phase cancellation technique, but with linear phase filters (to preserve phase). The phase cancellation trick will allow to cancel out pre-ringing as well as potential low-frequency imprecisions, and the usage of linear phase filters will prevent the introduction of unwanted frequencies when canceling (as discussed above). In the end, the additional delay will be the only price to pay for such a splitter.

Dan Worrall also has a video on the subject if you want to check that out.

Final considerations

No matter which technique is being used, there are some considerations we need to keep in mind that apply to all of them. In general, creating static frequency splitters like these may lead to phase issues when processing the bands with phase-altering effects. Since the effects are only applied to some bands and not all, the phase response of each band may become out-of-sync with the others, which may introduce unexpected results when combined back together. That’s why we can’t naively nest frequency splitters to generate more bands (as we’ve seen in The standard frequency splitter section).

Because of that, it’s generally recommended to use your ears or use effects that are phase agnostic. Sometimes, the difference is minimal, and other times it can be more obvious. Pro-MB and others work by using dynamic modes which only alter the phase response proportionally to the amount of gain difference, but this technique only works for their specific use case (multiband compression). Otherwise, we can treat the splitter as an effect itself and not care about any of this.

All in all, I usually use this sort of trick for individual sound design / processing, rather than mixing and bus processing (main groups, master, etc.). I would advise not using it on punchy or low-frequency elements as well, such as the kick and the sub-bass. If you do, try to avoid using too low crossovers and make sure to use your ears.

Conclusion

When implementing a frequency splitter, you should seek the following solutions (in order):

1. The standard frequency splitter
   • + Flat amplitude response
   • + Simple
   • + Low latency
   • + No phase cancellation tricks
   • + Can be implemented using most EQs
   • - Altered phase response
2. The almost perfect frequency splitter
   • + Flat amplitude response
   • + Flat phase response
   • + Reconstructs the exact input signal back
   • - Cannot be implemented using most EQs
   • - More complicated
   • - Higher latency
3. The standard frequency splitter using linear phase filters
   • + Flat phase response
   • + Simple
   • + No phase cancellation tricks
   • - May introduce pre-ringing (colored crossovers)
   • - May introduce low-frequency imprecisions (colored crossovers)
   • - Cannot be implemented using most EQs
   • - Higher latency

Here are the solutions you should avoid entirely:

1. The naive frequency splitter
   • + Simple
   • - Colored crossovers
   • - Altered phase response
2. The “phase correct” frequency splitter
   • + Reconstructs the exact input signal back
   • - Doesn’t work in isolation (i.e. individual bands)
   • - More complicated

As you can see, there’s not much to be gained from this clever phase cancellation trick. In practice, a standard Linkwitz-Riley frequency splitter is the way to go. It doesn’t involve any phase cancellation trick, it’s low latency and it works just fine. If you are working with phase-sensitive material, only then should you consider the phase cancellation trick (using linear phase filters exclusively) as an alternative.

Note that this post will be frequently updated, and a series of YouTube videos are coming along the way. Stay tuned, and feel free to share and comment in the meantime.

All the figures in this post have been made with Desmos and captured with GIFsmos V.